5. Examples
In the input file filename{numo3d.in} the test cases are controlled by the input parameter ‘icase’. h-NUMO contains the following ready-to-use test cases: begin{enumerate} item test_case = ‘bump’ is the perturbation in the bottom layer for the two-layer. item test_case = ‘double-gyre’ is a double-gyre test case. item test_case = ‘lakeAtrest’ is lake-at-rest test case. end{enumerate}
We present some examples of idealised modeling studies. To run these simulations change into the Examples/ directory.
5.1. test_case = ‘lakeAtrest’: Well-balanced test
This test case is used to validate the well-balanced property of the DG scheme for the multilayer equations. We have initialized the layers fluid domain with densities \(\rho_k = 1027.01037 + 0.2110\times (k-1) \frac{kg}{m^3}, \ k = 1,\ldots,N_l\) and the layer interface positions \(z_k = -40/N_l\) m, where \(N_l\) is the number of layers. The horizontal extend of the domain was \((x,y)\in [0,\ 2000]\times[0,\ 2000]\) m with wall boundary conditions on both ends, and the bottom topography is given by
where \(r = \sqrt{(x-1000)^2 + (y-1000)^2}\).
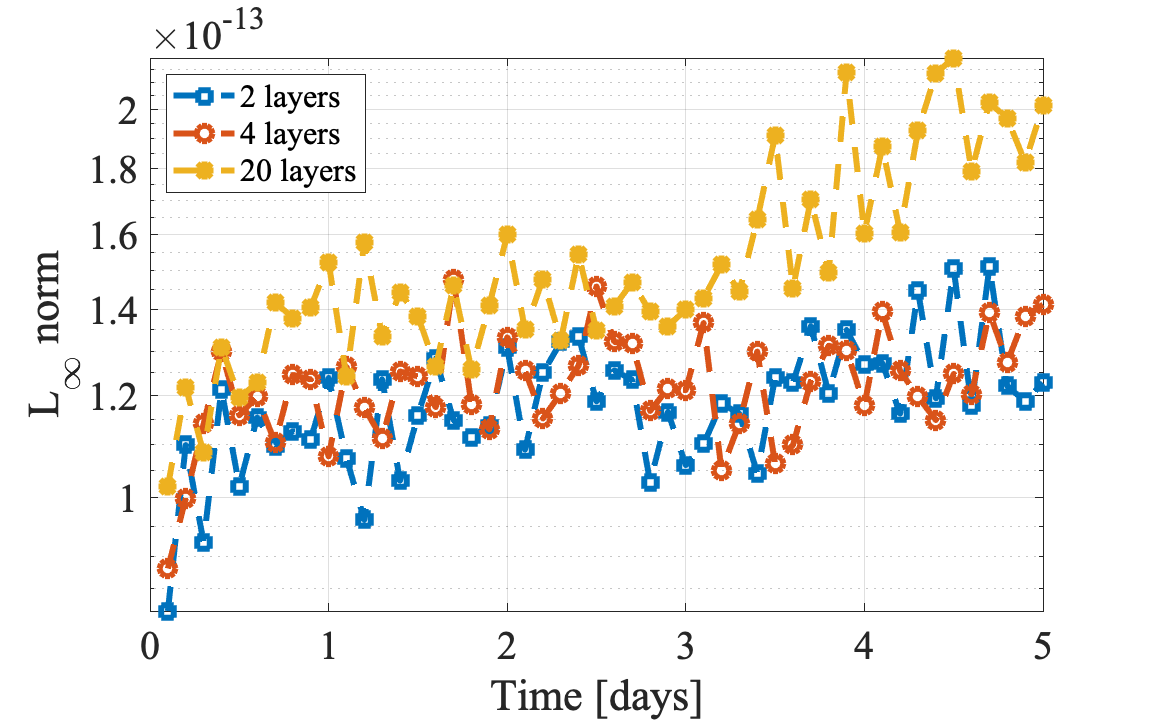
Figure 5.1 Cross-section of the free surface at time t = 3 hours

Figure 5.2 Infinity norm of the free surface solution over 5 days
5.2. test_case = ‘bump’: Baroclinic wave propagation
This test case consists of a two-layer system. To test whether our model captures the wave propagation speeds correctly, we consider a small perturbation in the interface between layers of the lake-at-rest case with a flat bottom topography. The layer initial interface positions are \(z_0 = 0\) m, \(z_1 = -20 + 0.5\left( 1 + \cos\left(\frac{\pi r}{250} \right)\right)\) m and \(z_2 = -40\) m. This test can be run with no-slip or free-slip boundary conditions, and more on these boundary conditions are in Sec.ref{sec:boundary_conditions}.
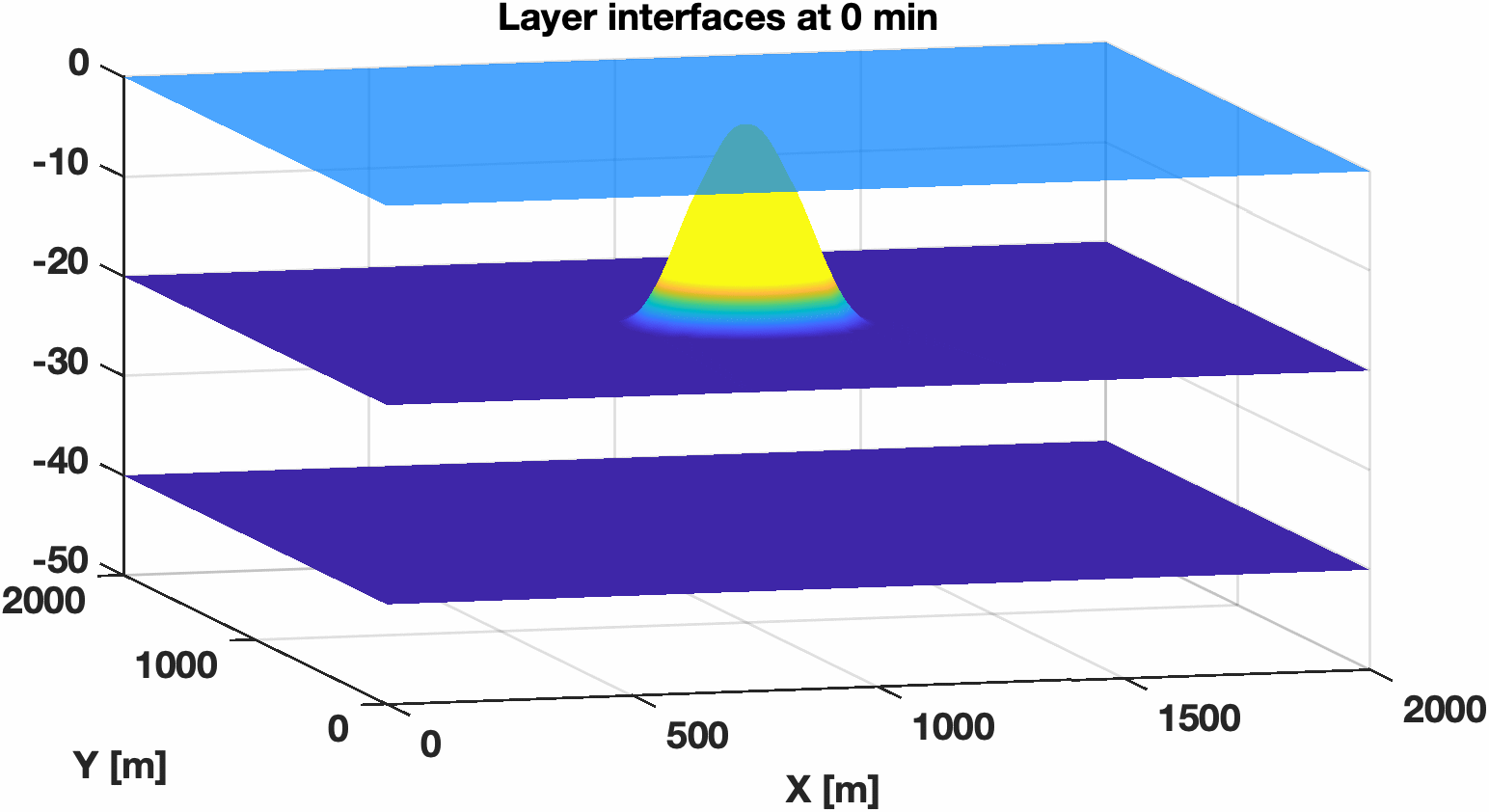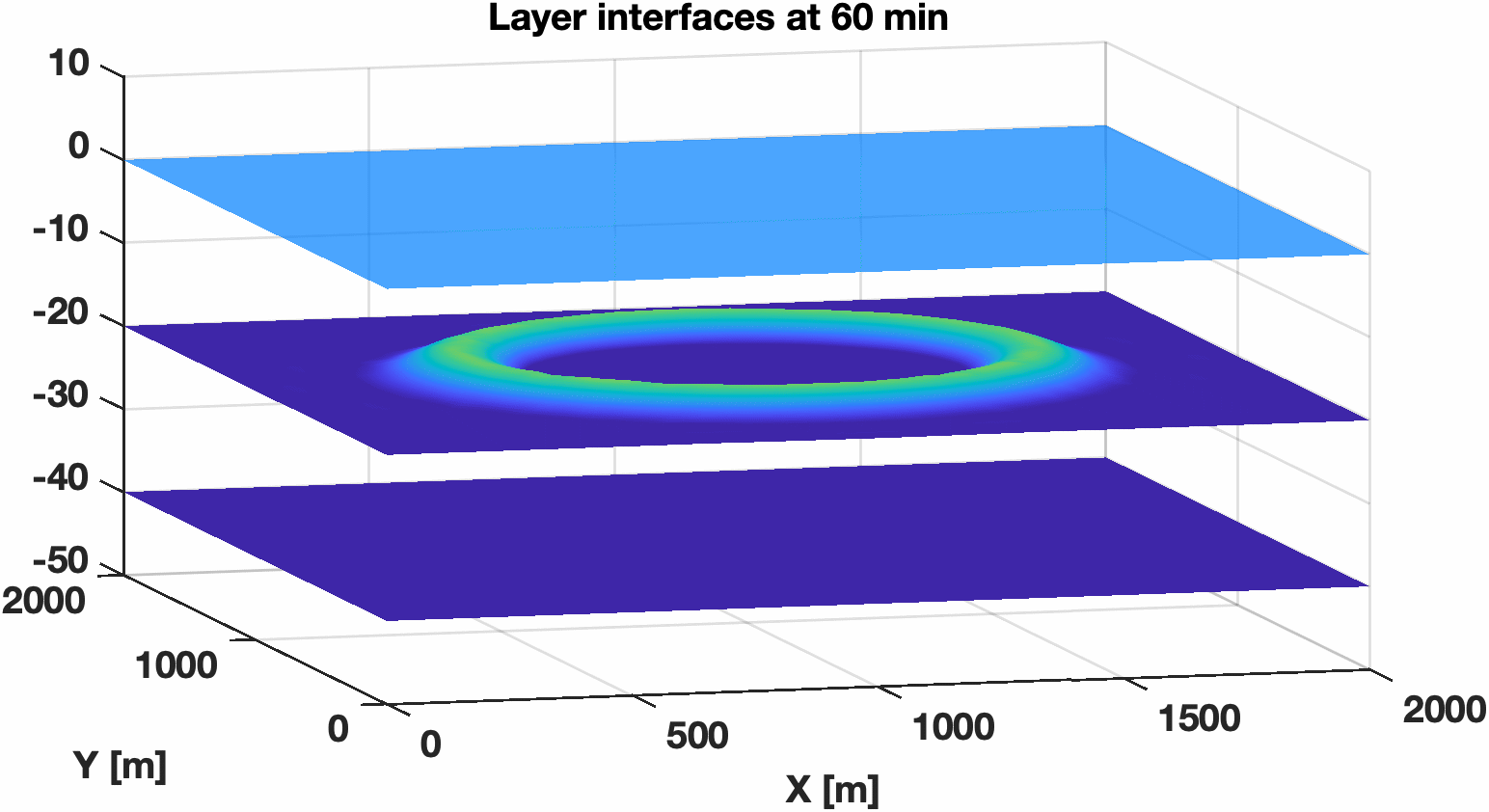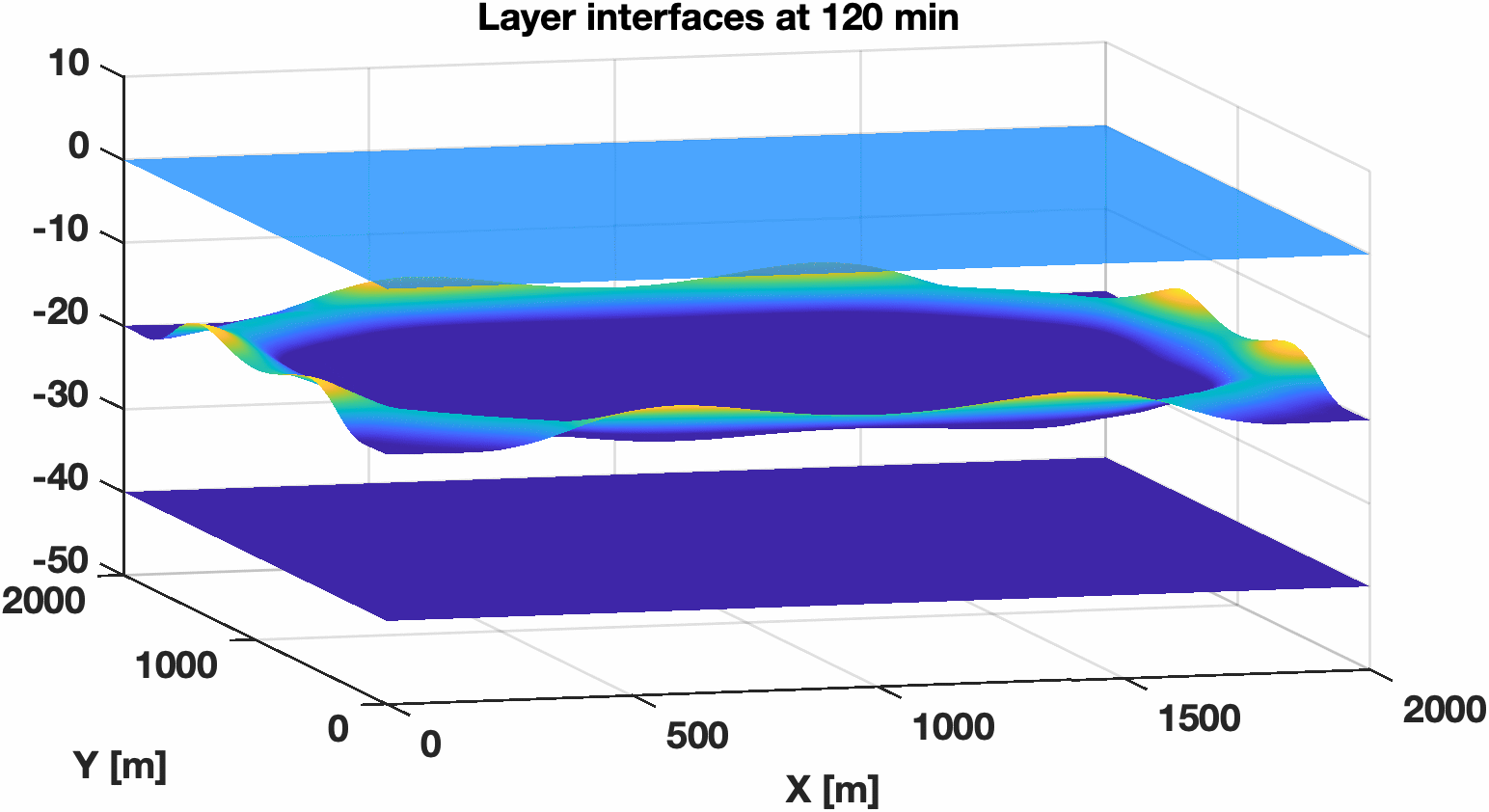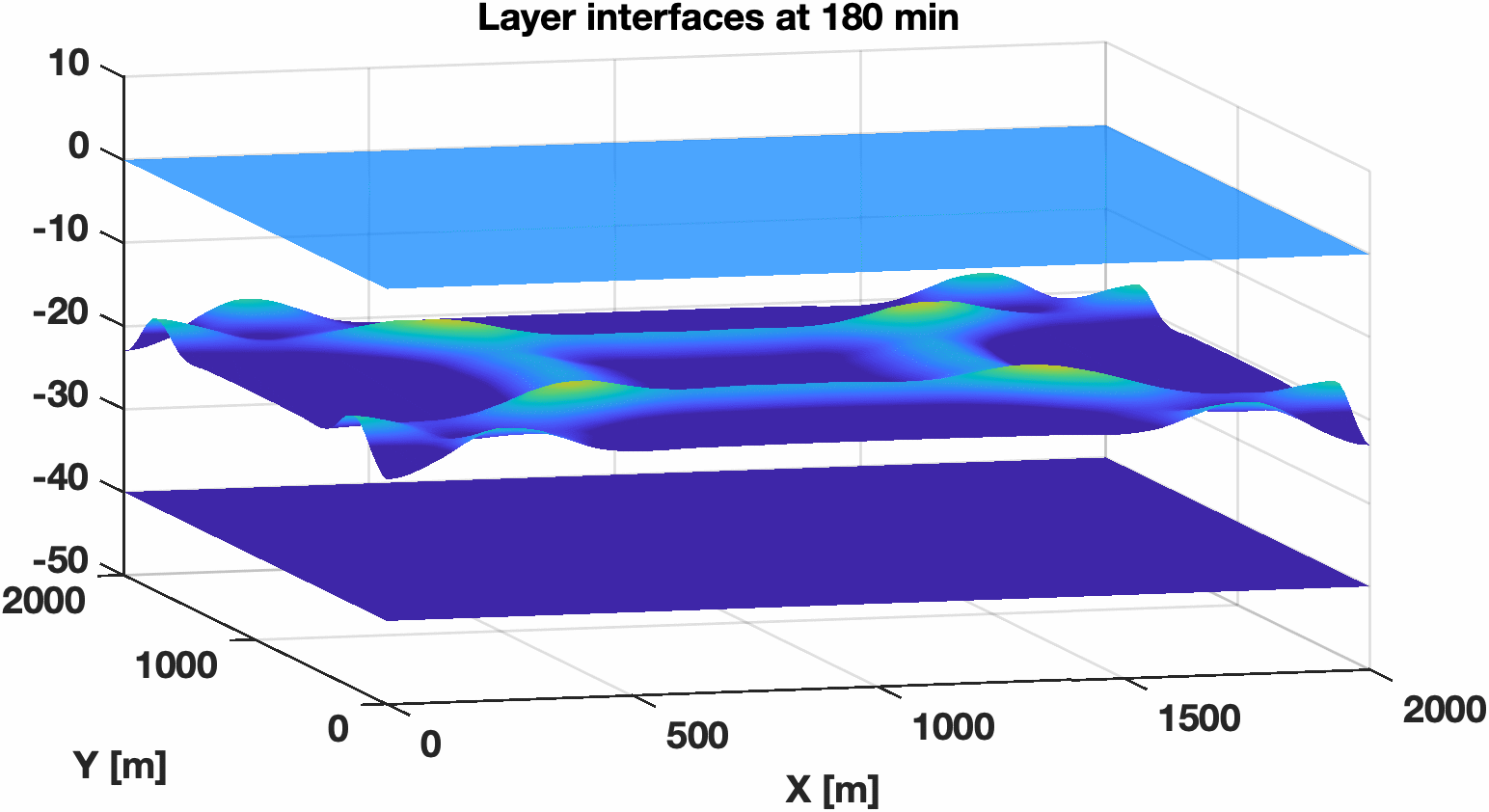
Figure 5.3 Free surface and interface of the second layer. The perturbation vertical scale is exaggerated in both panels.
5.3. test_case = ‘double-gyre’ Double-gyre test
This test case consists of an idealized double-gyre benchmark test [3] to validate h-NUMO ability to simulate the mesoscale and submesoscale processes and compare the results with HYCOM. The domain is a closed rectangular ocean basin with a flat bottom. The forcing is spatially varying wind stress with intense western boundary currents, which, together with Coriolis force, results in a counter-clockwise circulation in the northern part and a clockwise circulation in the southern part of the domain.
The horizontal extend is \(D = 2000\ km\) in both the zonal and the meridional direction. The depth of the basin is \(10\ km\) consisting of two layers, with the upper and lower layers initially having $:math:1.5km and \(8.5\ km\) depths respectively. The densities in the layers are \(\rho_1 = 1027.01037\ \ kg/m^3\) , \(\rho_2 = 1027.22136\ \ kg/m^3\). The Coriolis force is prescribed using a beta-plane approximation centered at \(45^\circ\) N, with a parameter \(f = f_0 + \beta(y-D/2)\), where \(f_0 = 9.3 \times 10^{-4} \ s^{-1}\) and \(\beta = 2 \times 10^{-11} \ m/s\). We consider two different values of the horizontal viscosity \(\nu = 50 \ m^2/s\) and \(\nu = 500 \ m^2/s\), the dimensionless bottom drag coefficient in the linear bottom stress is \(c_d = 10^{-7} \ s^{-1}\), and we assume no shear stress between layers. The system is forced by a purely zonal wind stress \(\tau = (\tau_x,\ \tau_y)\), where \(\tau_x = -\tau_0\cos(2\pi y/D)\), \(\tau_y = 0\ N/m^2\), and \(\tau_0 = 0.1 \ N/m^2\). We considered two different boundary conditions: free-slip and no-slip. Each model year consists of 360 days, divided into 12 months, with 30 days per month.
Figure 5.4 Sea surface height with h-NUMO and HYCOM using the free-slip boundary condition and viscosity \(\nu = 50\ m^2/s\). The contour interval is 2 centimeters, with lower elevations in the northern region and higher elevations in the southern region.